Starkex署名のPython実装を見てみる【dydxユーザー必見】

dydx v4に移行する前に久しぶりにdydxを触ってみようと思い、Starkexで使われる楕円曲線暗号の計算式を調べていたら公式ドキュメントから解説が消えていました。ということで、備忘録がてらに触れておきます。

( dydxもそろそろv4に移行する頃でしょうか...)

楕円曲線暗号(ECC)の概要

$y^2 = x^3+ ax + b$を満たすある有限体上の点$(x,y)$の集合にはベースポイントPがあり、これを複数回(n)加算してnPを求めます。このnPの値が公開鍵であり、nの値が秘密鍵です。

nとPの値が与えられた時、nPを求めるのは楕円曲線の加法を用いればコンピュータを使って求めることができます。 しかし、nPからnの値を求めるのは(量子コンピュータでもなければ)困難であり、これが楕円曲線暗号が成立している直感的理由となります。

---

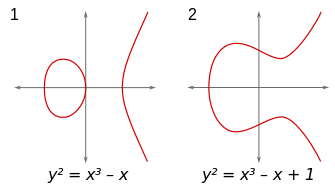
楕円曲線(wikipediaより引用)

では実際に　どうnとPからnPが求められるのかと言いますと、これには効率性の観点から点の加法$(R=P+Q)$というアプローチが用いられます。$2P=P+P$なので計算は高々定数倍のオーダーで実行できることがわかります。

$x^3+ ax + b \mod{p}$ 上で追加したい2 つの点 $P( x_1, y_1)$と $Q(x_2, y_2)$がある場合、それらの点の間の勾配sを計算します。

$$s =( y_1 − y_2)/( x_1 − x_2)$$

新しい点 $R(x_3,y_3)$を決定するためには

$$x_3 = s ²− x_1 − x_2$$ $$y_3 = s ( x_1 − x_2) − y_1$$

このように楕円曲線に直線をひくイメージで簡単に点と点の足し算は行えます。

PythonでのStark Curveの実装

楕円曲線暗号と言っても全ての楕円曲線が暗号に使われるわけではありません。楕円曲線式上のaとbの値の条件によってそれが安全性を担保できるのかどうか数学的に証明しなければなりません。

Starkexでは定数aとbの値を次のように定めています。ちなみに、効率性の観点から楕円曲線上の点はある素数pに対する剰余として計算していきます。

$$x^3 + ax + b \mod{p}$$ $$a = 1$$ $$b = 3141592653589793238462643383279502884197169399375105820974944592307816406665$$ $$p = 3618502788666131213697322783095070105623107215331596699973092056135872020481$$

この楕円曲線は元のメッセージのハッシュ化(Pedersen Hashというものを使います)、秘密鍵nを用いての署名、そして公開鍵nPを用いての検証の三つに使われます。

ではPythonの実装を見ていきましょう。コードはdydxの公式モジュールから拝借いたしました。

from sympy.core.numbers import igcdex

pedersen_param = PEDERSEN_PARAMS['CONSTANT_POINTS'] 

def div_mod(n: int, m: int, p: int) -> int:
    a, b, c = igcdex(m, p) 
    return (n * a) % p

def ec_add(point1, point2, p: int):
    m = div_mod(point1[1] - point2[1], point1[0] - point2[0], p)
    x = (m * m - point1[0] - point2[0]) % p
    y = (m * (point1[0] - x) - point1[1]) % p
    return x, y


def pedersen_hash(x:int, y:int):

    point = [2089986280348253421170679821480865132823066470938446095505822317253594081284,1713931329540660377023406109199410414810705867260802078187082345529207694986]
    for pt in pedersen_param[2 + 0 * 252:2 + (0 + 1) * 252]:
        if x & 1: point = ec_add(point, pt, 3618502788666131213697322783095070105623107215331596699973092056135872020481)
        x >>= 1 

    for pt in pedersen_param[2 + 1 * 252:2 + (1 + 1) * 252]:
        if y & 1: point = ec_add(point, pt, 3618502788666131213697322783095070105623107215331596699973092056135872020481)
        y >>= 1     
    
    return point[0]

Stark Curve上の定点となるPEDERSEN_PARAMSはPedersenパラメータから落としてきてください。

試しに次のようなオーダーを暗号化してみましょう。

EXPTIME = time.time() + 100

position_id = str(xxxxxx) #アカウントごとに紐つけられている６桁の数字
order_detail_example = {
    'network_id': 1,
    'position_id': position_id,
    'client_id': 'test_order1',
    'market': 'BTC-USD',
    'side': 'BUY',
    'size': '1.0',
    'price': '40000',
    'limit_fee': '0.01',
    'expiration_epoch_seconds': EXPTIME
}

公式Githubから直接コードを拝借いたします。ページに収まるようにディレクトリや変数をまとめて簡潔に書いています。

import Decimal

Resolution_MAP ={'BTC-USD':'10000000000', 'USDC':'1000000'}
InstrumentID_MAP = {'BTC-USD': 344400637343183300222065759427231744}

def get_order_hash(order_details:dict):
    instrument = order_details['market']

    size = int(Decimal(order_details['size'])  * Decimal(Resolution_MAP[instrument]))

    instrument_id = InstrumentID_MAP[instrument]

    cost = int(Decimal(Resolution_MAP['USDC']) * Decimal(order_details['price']) * Decimal(order_details['size']))
    limit_fee = int(cost * Decimal(order_details['limit_fee']))

    exp_time = math.ceil(float(order_details['expiration_epoch_seconds']) / 3600) + 168 #ORDER_SIGNATURE_EXPIRATION_BUFFER_HOURS

    nonce = int(hashlib.sha256(order_details['client_id'].encode('utf-8')).hexdigest(),16) % 4294967296 #NONCE_UPPER_BOUND_EXCLUSIVE

    if order_details['side'] == 'BUY':
        part_1 = cost
        part_1 <<= 64 #ORDER_FIELD_BIT_LENGTHS['quantums_amount']
        part_1 += size
        part_1 <<= 64 #ORDER_FIELD_BIT_LENGTHS['quantums_amount']
        part_1 += limit_fee
        part_1 <<= 32 #ORDER_FIELD_BIT_LENGTHS['nonce']
        part_1 += nonce

        assets_hash = pedersen_hash(pedersen_hash(CollateralID,instrument_id),CollateralID)

    elif order_details['side'] == 'SELL':
        part_1 = size
        part_1 <<= 64 #ORDER_FIELD_BIT_LENGTHS['quantums_amount']
        part_1 += cost
        part_1 <<= 64 #ORDER_FIELD_BIT_LENGTHS['quantums_amount']
        part_1 += limit_fee
        part_1 <<= 32 #ORDER_FIELD_BIT_LENGTHS['nonce']
        part_1 += nonce
        
        assets_hash = pedersen_hash(pedersen_hash(instrument_id,CollateralID),CollateralID)

    else:
        raise ValueError('Please use BUY or SELL')

    part_2 = 3 #Order Preferix


    part_2 <<= 64 #ORDER_FIELD_BIT_LENGTHS['position_id']
    part_2 += int(order_details['position_id'])


    part_2 <<= 64 #ORDER_FIELD_BIT_LENGTHS['position_id']
    part_2 += int(order_details['position_id'])


    part_2 <<= 64 #ORDER_FIELD_BIT_LENGTHS['position_id']
    part_2 += int(order_details['position_id'])


    part_2 <<= 32 #ORDER_FIELD_BIT_LENGTHS['expiration_epoch_hours']
    part_2 += exp_time

   
    part_2 <<= 17 #ORDER_PADDING_BITS


    return pedersen_hash(pedersen_hash(assets_hash,part_1),part_2)

大量のBit演算子が出てきてわかりにくいですが、やっていることはそれぞれBIT長の分だけシフトさせて情報を変数に詰め込んでいるようです。色々とある定数はdydx側で定義されているもののようです。

こうやってハッシュ化されたメッセージに秘密鍵を用いて署名していきます。楕円曲線暗号の場合、不可逆性を持つRとSという二つのパラメータが得られます。

PythonのコードはStarkexの実装を参考にしてください。ちなみにdydx公式もこの実装をそのまま使っています。

コードのsign()という関数を見てみますと、秘密鍵、ハッシュ化されたメッセージ、そして乱数に使われるシードを引数に取っていることがわかると思います。そしてsign()関数内で楕円曲線上の点に対して乗算を繰り返していることがわかると思います。

結構複雑ですが、メッセージのハッシュ化、そしてハッシュの暗号化（＝秘密鍵を用いての署名）というパターンは一般的な暗号の仕組みと変わりません。

さて、最後に暗号化にいかほど時間がかかるかローカルマシンで測ってましょう。一般的なCEXにメッセージを送る時に使われるsha256暗号のエンコードには自分のマシンで大体0.1ミリ秒も時間がかかりません。

import time
from starkex_resources.proxy import sign

start = time.time()
order_hash = get_order_hash(order_detail_example)

EPOCH = time.time() - start

print('ハッシュ化にかかる時間: ',EPOCH * 1000, 'mil second')

start = time.time()
sign(order_hash,PRIVATE_KEY)
EPOCH = time.time() - start

print('署名にかかる時間: ',EPOCH * 1000, 'mil second')

ハッシュ化にかかる時間:  29.983997344970703 mil second
署名にかかる時間:  15.759706497192383 mil second

CEXへのオーダーと異なり、それぞれの注文の情報をStarkexで暗号化するため、かなり時間がかかります。。

結論

dydx v3でbot運用するならレイテンシーには気をつけること。ちゃんとコードは非同期通信させよう。